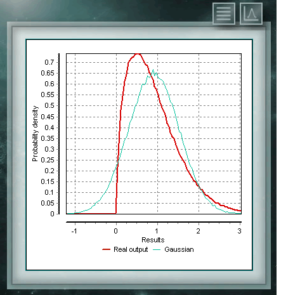
Это распределение является непрерывной функцией в области положительных вещественных чисел, часто используемой в экономике, метеорологии и телекоммуникациях, а также в других конкретных приложениях, таких как уровень надежности или выживаемость организмов или машин. Случайные переменные, имеющие распределение распределения Вейбулла, распределяют ошибки в системах, когда коэффициент ошибки пропорционально связан с мощностью времени. Это распределение определяется из характеристического параметра формы (& gt; 0), который указывает на частоту отказа, так что, если скорость отказа уменьшается, она является постоянной или увеличивается со временем. Это соответствует, если параметр k меньше, равен или больше 1.
Входные параметры:
- Форма. Этот параметр определяет форму распределения. Вы можете взять в качестве значения любое число полей чисел больше нуля.
- Масштаб. Этот второй параметр позволяет масштабировать результирующие значения, генерирующие псевдослучайные с одинаковой формой, но большее стандартное отклонение.
Дополнительная помощь
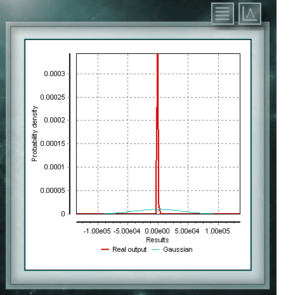Распределение Коши имеет особенность существования гауссовского типа распределений, однако оно имеет самый высокий пик, а хвосты разлагаются очень медленно. Хотя MCM Alchimia соответствующим образом генерирует псевдослучайные выборки для этого распределения, график результатов будет выглядеть как изолированный пик, поскольку ось абсцисс его берется в 99% -ном интервале вероятности покрытия. Поскольку распад хвостов настолько постепенный, диапазон значительных вероятностей становится очень узким.
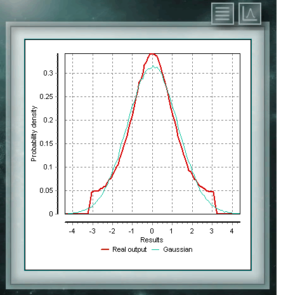Распределение фон Мизеса является непрерывной функцией круговых вызовов, т. Е. Они определены для реальных в интервале от 0 до 2π. В настоящее время эта функция используется предпочтительно в области эпидемиологии для описания распространения заболеваний или технологических применений, таких как обработка сигналов. Распространение фон Мизеса также известно как нормальный круговой , поскольку он подобен гауссову, но ограничен круговой плоскостью.
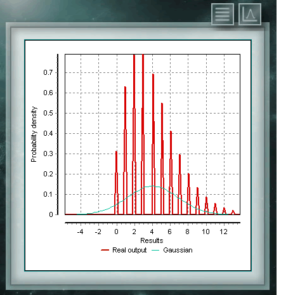Распределение Отрицательное биномиальное также является дискретным распределением, определенным в области положительных целых чисел. Он аналогичен биномиальному распределению, за исключением того, что параметр n относится к неточным и неполным событиям. Другими словами, случайная величина с Отрицательное биномиальное распределением параметров n и p представляет собой число успехов, вероятность которых равна p, которые достигаются в последовательности n неудачных испытаний. Параметры, с помощью которых определяется это распределение, имеют тот же вид, что и те, которые представляют биномиальное распределение, хотя, как мы сказали, параметр n представляет другое качество.
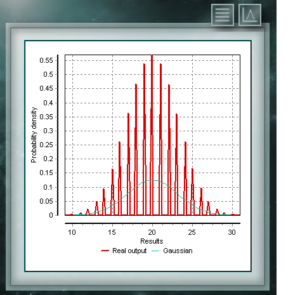Это дискретное распределение, домен которого является множеством положительных целых чисел, что представляет собой количество успехов, достигнутых в последовательности из n испытаний. Эти тесты должны иметь дихотомическую характеристику, т. Е. Предлагать в результате две возможности (успех и неудачу) и иметь определенную вероятность успеха = p.
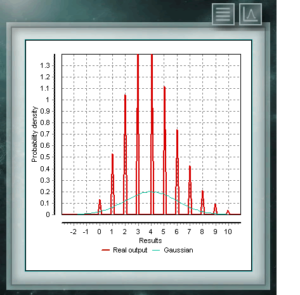Распределение Пуассона является дискретным распределением, определенным для области целых чисел, больших нуля. Он используется в основном для представления вероятности того, что определенное количество событий произойдет через определенный промежуток времени, определенное расстояние, площадь, объем и т. Д.
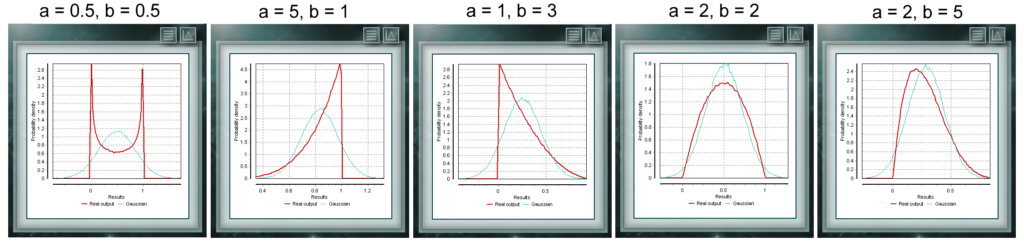Это распределение является непрерывной функцией с двумя параметрами, которые должны принимать реальные значения, большие нуля. Функция определяется между 0 и 1. Частный случай бета-распределения — это когда оба параметра формы принимают значения = 1. В этом случае функция будет совпадать с равномерным распределением.
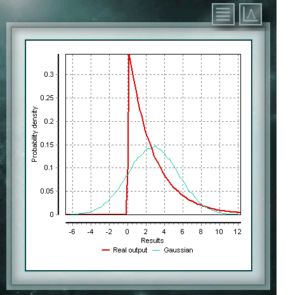Экспоненциальное распределение вероятностей является непрерывной функцией в области положительных чисел, что подходит для представления времени между двумя событиями, распределенными в соответствии с распределением пуассонов. Например, до тех пор, пока торговля не получит своего первого клиента в тот день. Экспоненциальное распределение является частным случаем распределения Гамма, где параметр формы принимает значение 1.
Это распределение является непрерывной функцией смещенного характера, то есть, когда модальное значение не соответствует среднему значению. Распределение Гамма является обобщением экспоненциального распределения и используется в общем случае для моделирования случайных величин, которые представляют время, в течение которого событие происходит определенное количество раз.